Crude periodicity finding

Discover the periods in evolution of animal populations (../../../../data/populations.txt)

Load the data

import numpy as np

data = np.loadtxt("../../../../data/populations.txt")
years = data[:, 0]
populations = data[:, 1:]

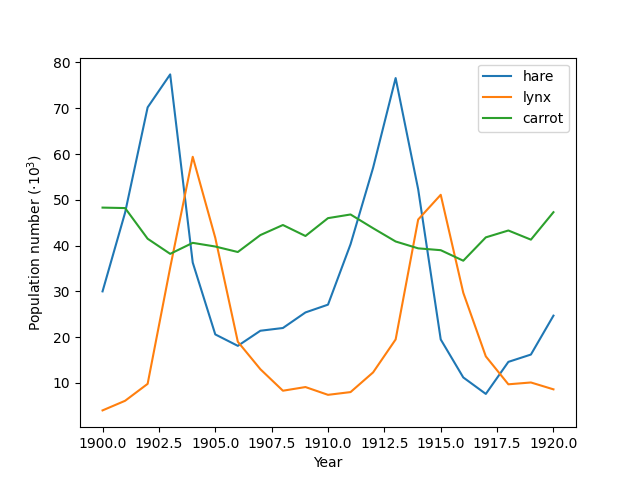
Plot the data

import matplotlib.pyplot as plt

plt.figure()
plt.plot(years, populations * 1e-3)
plt.xlabel("Year")
plt.ylabel(r"Population number ($\cdot10^3$)")
plt.legend(["hare", "lynx", "carrot"], loc=1)

<matplotlib.legend.Legend object at 0x7f0935627b90>

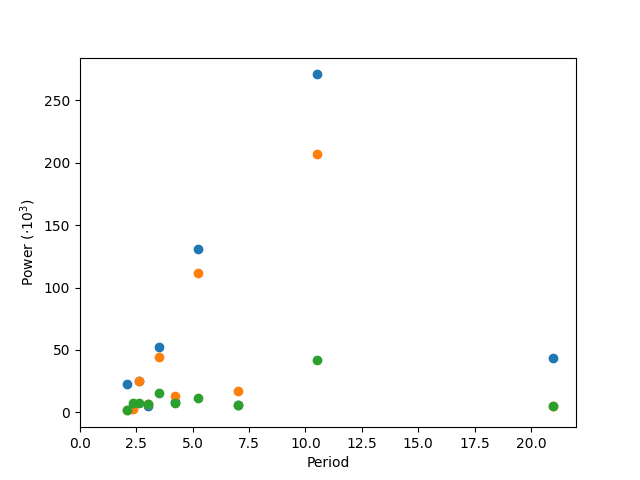
Plot its periods

import scipy as sp

ft_populations = sp.fft.fft(populations, axis=0)
frequencies = sp.fft.fftfreq(populations.shape[0], years[1] - years[0])
periods = 1 / frequencies

plt.figure()
plt.plot(periods, abs(ft_populations) * 1e-3, "o")
plt.xlim(0, 22)
plt.xlabel("Period")
plt.ylabel(r"Power ($\cdot10^3$)")

plt.show()

/home/runner/work/scientific-python-lectures/scientific-python-lectures/intro/scipy/examples/solutions/plot_periodicity_finder.py:39: RuntimeWarning: divide by zero encountered in divide
  periods = 1 / frequencies

There’s probably a period of around 10 years (obvious from the plot), but for this crude a method, there’s not enough data to say much more.