2.2. Advanced NumPy

Author: Pauli Virtanen

NumPy is at the base of Python’s scientific stack of tools. Its purpose to implement efficient operations on many items in a block of memory. Understanding how it works in detail helps in making efficient use of its flexibility, taking useful shortcuts.

This section covers:

  • Anatomy of NumPy arrays, and its consequences. Tips and tricks.

  • Universal functions: what, why, and what to do if you want a new one.

  • Integration with other tools: NumPy offers several ways to wrap any data in an ndarray, without unnecessary copies.

  • Recently added features, and what’s in them: PEP 3118 buffers, generalized ufuncs, …

Tip

In this section, NumPy will be imported as follows:

>>> import numpy as np

2.2.1. Life of ndarray

2.2.1.1. It’s…

ndarray =

block of memory + indexing scheme + data type descriptor

  • raw data

  • how to locate an element

  • how to interpret an element

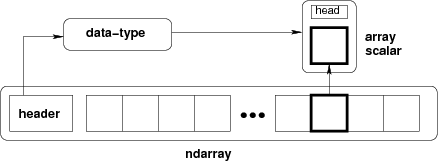
../../_images/threefundamental.png 
typedef struct PyArrayObject {

        PyObject_HEAD



        /* Block of memory */

        char *data;



        /* Data type descriptor */

        PyArray_Descr *descr;



        /* Indexing scheme */

        int nd;

        npy_intp *dimensions;

        npy_intp *strides;



        /* Other stuff */

        PyObject *base;

        int flags;

        PyObject *weakreflist;

} PyArrayObject;

2.2.1.2. Block of memory

>>> x = np.array([1, 2, 3], dtype=np.int32)

>>> x.data

<... at ...>

>>> bytes(x.data)

b'\x01\x00\x00\x00\x02\x00\x00\x00\x03\x00\x00\x00'

Memory address of the data:

>>> x.__array_interface__['data'][0] 

64803824

The whole __array_interface__:

>>> x.__array_interface__

{'data': (..., False), 'strides': None, 'descr': [('', '<i4')], 'typestr': '<i4', 'shape': (3,), 'version': 3}

Reminder: two ndarrays may share the same memory:

>>> x = np.array([1, 2, 3, 4])

>>> y = x[:-1]

>>> x[0] = 9

>>> y

array([9, 2, 3])

Memory does not need to be owned by an ndarray:

>>> x = b'1234'

x is a string (in Python 3 a bytes), we can represent its data as an array of ints:

>>> y = np.frombuffer(x, dtype=np.int8)

>>> y.data

<... at ...>

>>> y.base is x

True



>>> y.flags

  C_CONTIGUOUS : True

  F_CONTIGUOUS : True

  OWNDATA : False

  WRITEABLE : False

  ALIGNED : True

  WRITEBACKIFCOPY : False

The owndata and writeable flags indicate status of the memory block.

See also

array interface

2.2.1.3. Data types

The descriptor

dtype describes a single item in the array:

type

scalar type of the data, one of:

int8, int16, float64, et al. (fixed size)

str, unicode, void (flexible size)

itemsize

size of the data block

byteorder

byte order: big-endian > / little-endian < / not applicable |

fields

sub-dtypes, if it’s a structured data type

shape

shape of the array, if it’s a sub-array

 
>>> np.dtype(int).type

<class 'numpy.int64'>

>>> np.dtype(int).itemsize

8

>>> np.dtype(int).byteorder

'='

Example: reading .wav files

The .wav file header:

chunk_id

"RIFF"

chunk_size

4-byte unsigned little-endian integer

format

"WAVE"

fmt_id

"fmt "

fmt_size

4-byte unsigned little-endian integer

audio_fmt

2-byte unsigned little-endian integer

num_channels

2-byte unsigned little-endian integer

sample_rate

4-byte unsigned little-endian integer

byte_rate

4-byte unsigned little-endian integer

block_align

2-byte unsigned little-endian integer

bits_per_sample

2-byte unsigned little-endian integer

data_id

"data"

data_size

4-byte unsigned little-endian integer

  • 44-byte block of raw data (in the beginning of the file)

  • … followed by data_size bytes of actual sound data.

The .wav file header as a NumPy structured data type:

>>> wav_header_dtype = np.dtype([

...     ("chunk_id", (bytes, 4)), # flexible-sized scalar type, item size 4

...     ("chunk_size", "<u4"),    # little-endian unsigned 32-bit integer

...     ("format", "S4"),         # 4-byte string

...     ("fmt_id", "S4"),

...     ("fmt_size", "<u4"),

...     ("audio_fmt", "<u2"),     #

...     ("num_channels", "<u2"),  # .. more of the same ...

...     ("sample_rate", "<u4"),   #

...     ("byte_rate", "<u4"),

...     ("block_align", "<u2"),

...     ("bits_per_sample", "<u2"),

...     ("data_id", ("S1", (2, 2))), # sub-array, just for fun!

...     ("data_size", "u4"),

...     #

...     # the sound data itself cannot be represented here:

...     # it does not have a fixed size

...    ])

See also

wavreader.py

>>> wav_header_dtype['format']

dtype('S4')

>>> wav_header_dtype.fields

mappingproxy({'chunk_id': (dtype('S4'), 0), 'chunk_size': (dtype('uint32'), 4), 'format': (dtype('S4'), 8), 'fmt_id': (dtype('S4'), 12), 'fmt_size': (dtype('uint32'), 16), 'audio_fmt': (dtype('uint16'), 20), 'num_channels': (dtype('uint16'), 22), 'sample_rate': (dtype('uint32'), 24), 'byte_rate': (dtype('uint32'), 28), 'block_align': (dtype('uint16'), 32), 'bits_per_sample': (dtype('uint16'), 34), 'data_id': (dtype(('S1', (2, 2))), 36), 'data_size': (dtype('uint32'), 40)})

>>> wav_header_dtype.fields['format']

(dtype('S4'), 8)

  • The first element is the sub-dtype in the structured data, corresponding to the name format

  • The second one is its offset (in bytes) from the beginning of the item

>>> f = open('data/test.wav', 'r')

>>> wav_header = np.fromfile(f, dtype=wav_header_dtype, count=1)

>>> f.close()

>>> print(wav_header)   

[ ('RIFF', 17402L, 'WAVE', 'fmt ', 16L, 1, 1, 16000L, 32000L, 2, 16, [['d', 'a'], ['t', 'a']], 17366L)]

>>> wav_header['sample_rate']

array([16000], dtype=uint32)

Let’s try accessing the sub-array:

>>> wav_header['data_id']  

array([[['d', 'a'],

        ['t', 'a']]],

      dtype='|S1')

>>> wav_header.shape

(1,)

>>> wav_header['data_id'].shape

(1, 2, 2)

When accessing sub-arrays, the dimensions get added to the end!

Note

There are existing modules such as wavfile, audiolab, etc. for loading sound data…

Casting and re-interpretation/views

casting

  • on assignment

  • on array construction

  • on arithmetic

  • etc.

  • and manually: .astype(dtype)

data re-interpretation

  • manually: .view(dtype)

Casting

  • Casting in arithmetic, in nutshell:

    • only type (not value!) of operands matters

    • largest “safe” type able to represent both is picked

    • scalars can “lose” to arrays in some situations

  • Casting in general copies data:

    >>> x = np.array([1, 2, 3, 4], dtype=float)

    >>> x

    array([1.,  2.,  3.,  4.])

    >>> y = x.astype(np.int8)

    >>> y

    array([1, 2, 3, 4], dtype=int8)

    >>> y + 1

    array([2, 3, 4, 5], dtype=int8)

    >>> y + 256

    Traceback (most recent call last):

      File "<stdin>", line 1, in <module>

    OverflowError: Python integer 256 out of bounds for int8

    >>> y + 256.0

    array([257.,  258.,  259.,  260.])

    >>> y + np.array([256], dtype=np.int32)

    array([257, 258, 259, 260], dtype=int32)

  • Casting on setitem: dtype of the array is not changed on item assignment:

    >>> y[:] = y + 1.5

    >>> y

    array([2, 3, 4, 5], dtype=int8)

Note

Exact rules: see NumPy documentation

Re-interpretation / viewing

  • Data block in memory (4 bytes)

    0x01

    ||

    0x02

    ||

    0x03

    ||

    0x04

    • 4 of uint8, OR,

    • 4 of int8, OR,

    • 2 of int16, OR,

    • 1 of int32, OR,

    • 1 of float32, OR,

    • …

    How to switch from one to another?

  1. Switch the dtype:

    >>> x = np.array([1, 2, 3, 4], dtype=np.uint8)

    >>> x.dtype = "<i2"

    >>> x

    array([ 513, 1027], dtype=int16)

    >>> 0x0201, 0x0403

    (513, 1027)

0x01

0x02

||

0x03

0x04

Note

little-endian: least significant byte is on the left in memory

  1. Create a new view of type uint32, shorthand i4:

    >>> y = x.view("<i4")

    >>> y

    array([67305985], dtype=int32)

    >>> 0x04030201

    67305985

0x01

0x02

0x03

0x04

Note

  • .view() makes views, does not copy (or alter) the memory block

  • only changes the dtype (and adjusts array shape):

    >>> x[1] = 5

    >>> y

    array([328193], dtype=int32)

    >>> y.base is x

    True

Mini-exercise: data re-interpretation

See also

view-colors.py

You have RGBA data in an array:

>>> x = np.zeros((10, 10, 4), dtype=np.int8)

>>> x[:, :, 0] = 1

>>> x[:, :, 1] = 2

>>> x[:, :, 2] = 3

>>> x[:, :, 3] = 4

where the last three dimensions are the R, B, and G, and alpha channels.

How to make a (10, 10) structured array with field names ‘r’, ‘g’, ‘b’, ‘a’ without copying data?

>>> y = ...                     



>>> assert (y['r'] == 1).all()  

>>> assert (y['g'] == 2).all()  

>>> assert (y['b'] == 3).all()  

>>> assert (y['a'] == 4).all()

Solution

...

Warning

Another two arrays, each occupying exactly 4 bytes of memory:

>>> x = np.array([[1, 3], [2, 4]], dtype=np.uint8)

>>> x

array([[1, 3],

       [2, 4]], dtype=uint8)

>>> y = x.transpose()

>>> y

array([[1, 2],

       [3, 4]], dtype=uint8)

We view the elements of x (1 byte each) as int16 (2 bytes each):

>>> x.view(np.int16)

array([[ 769],

       [1026]], dtype=int16)

What is happening here? Take a look at the bytes stored in memory by x:

>>> x.tobytes()

b'\x01\x03\x02\x04'

The \x stands for heXadecimal, so what we are seeing is:

0x01 0x03 0x02 0x04

We ask NumPy to interpret these bytes as elements of dtype int16—each of which occupies two bytes in memory. Therefore, 0x01 0x03 becomes the first uint16 and 0x02 0x04 the second.

You may then expect to see 0x0103 (259, when converting from hexadecimal to decimal) as the first result. But your computer likely stores most significant bytes first, and as such reads the number as 0x0301 or 769 (go on and type 0x0301 into your Python terminal to verify).

We can do the same on a copy of y (why doesn’t it work on y directly?):

>>> y.copy().view(np.int16)

array([[ 513],

       [1027]], dtype=int16)

Can you explain these numbers, 513 and 1027, as well as the output shape of the resulting array?

2.2.1.4. Indexing scheme: strides

Main point

The question:

>>> x = np.array([[1, 2, 3],

...               [4, 5, 6],

...               [7, 8, 9]], dtype=np.int8)

>>> x.tobytes('A')

b'\x01\x02\x03\x04\x05\x06\x07\x08\t'



At which byte in ``x.data`` does the item ``x[1, 2]`` begin?

The answer (in NumPy)

  • strides: the number of bytes to jump to find the next element

  • 1 stride per dimension

>>> x.strides

(3, 1)

>>> byte_offset = 3 * 1 + 1 * 2  # to find x[1, 2]

>>> x.flat[byte_offset]

np.int8(6)

>>> x[1, 2]

np.int8(6)

simple, flexible

C and Fortran order

Note

The Python built-in bytes returns bytes in C-order by default which can cause confusion when trying to inspect memory layout. We use numpy.ndarray.tobytes() with order=A instead, which preserves the C or F ordering of the bytes in memory.

>>> x = np.array([[1, 2, 3],

...               [4, 5, 6]], dtype=np.int16, order='C')

>>> x.strides

(6, 2)

>>> x.tobytes('A')

b'\x01\x00\x02\x00\x03\x00\x04\x00\x05\x00\x06\x00'

  • Need to jump 6 bytes to find the next row

  • Need to jump 2 bytes to find the next column

>>> y = np.array(x, order='F')

>>> y.strides

(2, 4)

>>> y.tobytes('A')

b'\x01\x00\x04\x00\x02\x00\x05\x00\x03\x00\x06\x00'

  • Need to jump 2 bytes to find the next row

  • Need to jump 4 bytes to find the next column

  • Similarly to higher dimensions:

    • C: last dimensions vary fastest (= smaller strides)

    • F: first dimensions vary fastest

    \mathrm{shape} &= (d_1, d_2, ..., d_n) \\ \mathrm{strides} &= (s_1, s_2, ..., s_n) \\ s_j^C &= d_{j+1} d_{j+2} ... d_{n} \times \mathrm{itemsize} \\ s_j^F &= d_{1} d_{2} ... d_{j-1} \times \mathrm{itemsize}

Note

Now we can understand the behavior of .view():

>>> y = np.array([[1, 3], [2, 4]], dtype=np.uint8).transpose()

>>> x = y.copy()

Transposition does not affect the memory layout of the data, only strides

>>> x.strides

(2, 1)

>>> y.strides

(1, 2)

>>> x.tobytes('A')

b'\x01\x02\x03\x04'

>>> y.tobytes('A')

b'\x01\x03\x02\x04'

  • the results are different when interpreted as 2 of int16

  • .copy() creates new arrays in the C order (by default)

Note

In-place operations with views

Prior to NumPy version 1.13, in-place operations with views could result in incorrect results for large arrays. Since version 1.13, NumPy includes checks for memory overlap to guarantee that results are consistent with the non in-place version (e.g. a = a + a.T produces the same result as a += a.T). Note however that this may result in the data being copied (as if using a += a.T.copy()), ultimately resulting in more memory being used than might otherwise be expected for in-place operations!

Slicing with integers

  • Everything can be represented by changing only shape, strides, and possibly adjusting the data pointer!

  • Never makes copies of the data

>>> x = np.array([1, 2, 3, 4, 5, 6], dtype=np.int32)

>>> y = x[::-1]

>>> y

array([6, 5, 4, 3, 2, 1], dtype=int32)

>>> y.strides

(-4,)



>>> y = x[2:]

>>> y.__array_interface__['data'][0] - x.__array_interface__['data'][0]

8



>>> x = np.zeros((10, 10, 10), dtype=float)

>>> x.strides

(800, 80, 8)

>>> x[::2,::3,::4].strides

(1600, 240, 32)

  • Similarly, transposes never make copies (it just swaps strides):

    >>> x = np.zeros((10, 10, 10), dtype=float)

    >>> x.strides

    (800, 80, 8)

    >>> x.T.strides

    (8, 80, 800)

But: not all reshaping operations can be represented by playing with strides:

>>> a = np.arange(6, dtype=np.int8).reshape(3, 2)

>>> b = a.T

>>> b.strides

(1, 2)

So far, so good. However:

>>> bytes(a.data)

b'\x00\x01\x02\x03\x04\x05'

>>> b

array([[0, 2, 4],

       [1, 3, 5]], dtype=int8)

>>> c = b.reshape(3*2)

>>> c

array([0, 2, 4, 1, 3, 5], dtype=int8)

Here, there is no way to represent the array c given one stride and the block of memory for a. Therefore, the reshape operation needs to make a copy here.

Example: fake dimensions with strides

Stride manipulation

>>> from numpy.lib.stride_tricks import as_strided

>>> help(as_strided)

Help on function as_strided in module numpy.lib.stride_tricks:

...

Warning

as_strided does not check that you stay inside the memory block bounds…

>>> x = np.array([1, 2, 3, 4], dtype=np.int16)

>>> as_strided(x, strides=(2*2, ), shape=(2, ))

array([1, 3], dtype=int16)

>>> x[::2]

array([1, 3], dtype=int16)

See also

stride-fakedims.py

Exercise

array([1, 2, 3, 4], dtype=np.int8)



-> array([[1, 2, 3, 4],

          [1, 2, 3, 4],

          [1, 2, 3, 4]], dtype=np.int8)

using only as_strided.:

Hint: byte_offset = stride[0]*index[0] + stride[1]*index[1] + ...

Spoiler

...

Broadcasting

  • Doing something useful with it: outer product of [1, 2, 3, 4] and [5, 6, 7]

>>> x = np.array([1, 2, 3, 4], dtype=np.int16)

>>> x2 = as_strided(x, strides=(0, 1*2), shape=(3, 4))

>>> x2

array([[1, 2, 3, 4],

       [1, 2, 3, 4],

       [1, 2, 3, 4]], dtype=int16)

>>> y = np.array([5, 6, 7], dtype=np.int16)

>>> y2 = as_strided(y, strides=(1*2, 0), shape=(3, 4))

>>> y2

array([[5, 5, 5, 5],

       [6, 6, 6, 6],

       [7, 7, 7, 7]], dtype=int16)

>>> x2 * y2

array([[ 5, 10, 15, 20],

       [ 6, 12, 18, 24],

       [ 7, 14, 21, 28]], dtype=int16)

… seems somehow familiar …

>>> x = np.array([1, 2, 3, 4], dtype=np.int16)

>>> y = np.array([5, 6, 7], dtype=np.int16)

>>> x[np.newaxis,:] * y[:,np.newaxis]

array([[ 5, 10, 15, 20],

       [ 6, 12, 18, 24],

       [ 7, 14, 21, 28]], dtype=int16)

  • Internally, array broadcasting is indeed implemented using 0-strides.

More tricks: diagonals

See also

stride-diagonals.py

Challenge

  • Pick diagonal entries of the matrix: (assume C memory order):

    >>> x = np.array([[1, 2, 3],

    ...               [4, 5, 6],

    ...               [7, 8, 9]], dtype=np.int32)

    

    >>> x_diag = as_strided(x, shape=(3,), strides=(???,))

  • Pick the first super-diagonal entries [2, 6].

  • And the sub-diagonals?

(Hint to the last two: slicing first moves the point where striding

starts from.)

Solution

...

See also

stride-diagonals.py

Challenge

Compute the tensor trace:

>>> x = np.arange(5*5*5*5).reshape(5, 5, 5, 5)

>>> s = 0

>>> for i in range(5):

...    for j in range(5):

...       s += x[j, i, j, i]

by striding, and using sum() on the result.

>>> y = as_strided(x, shape=(5, 5), strides=(TODO, TODO))   

>>> s2 = ...   

>>> assert s == s2

Solution

...

CPU cache effects

Memory layout can affect performance:

In [1]: x = np.zeros((20000,))



In [2]: y = np.zeros((20000*67,))[::67]



In [3]: x.shape, y.shape

Out[3]: ((20000,), (20000,))



In [4]: %timeit x.sum()

5.27 us +- 13.2 ns per loop (mean +- std. dev. of 7 runs, 100,000 loops each)



In [5]: %timeit y.sum()

23.5 us +- 39 ns per loop (mean +- std. dev. of 7 runs, 10,000 loops each)



In [6]: x.strides, y.strides

Out[6]: ((8,), (536,))

Smaller strides are faster?

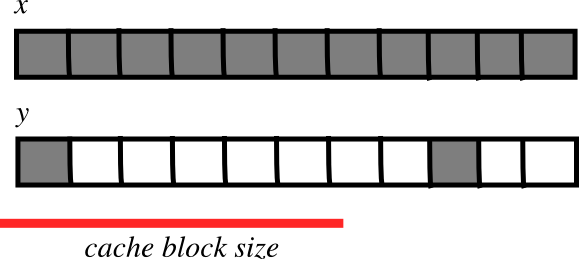
../../_images/cpu-cacheline.png

  • CPU pulls data from main memory to its cache in blocks

  • If many array items consecutively operated on fit in a single block (small stride):

    • \Rightarrow fewer transfers needed

    • \Rightarrow faster

See also

  • numexpr is designed to mitigate cache effects when evaluating array expressions.

  • numba is a compiler for Python code, that is aware of numpy arrays.

2.2.1.5. Findings in dissection

../../_images/threefundamental.png

  • memory block: may be shared, .base, .data

  • data type descriptor: structured data, sub-arrays, byte order, casting, viewing, .astype(), .view()

  • strided indexing: strides, C/F-order, slicing w/ integers, as_strided, broadcasting, stride tricks, diag, CPU cache coherence

2.2.2. Universal functions

2.2.2.1. What they are?

  • Ufunc performs and elementwise operation on all elements of an array.

    Examples:

    np.add, np.subtract, scipy.special.*, ...

  • Automatically support: broadcasting, casting, …

  • The author of an ufunc only has to supply the elementwise operation, NumPy takes care of the rest.

  • The elementwise operation needs to be implemented in C (or, e.g., Cython)

Parts of an Ufunc

  1. Provided by user

    void ufunc_loop(void **args, int *dimensions, int *steps, void *data)

    {

        /*

         * int8 output = elementwise_function(int8 input_1, int8 input_2)

         *

         * This function must compute the ufunc for many values at once,

         * in the way shown below.

         */

        char *input_1 = (char*)args[0];

        char *input_2 = (char*)args[1];

        char *output = (char*)args[2];

        int i;

    

        for (i = 0; i < dimensions[0]; ++i) {

            *output = elementwise_function(*input_1, *input_2);

            input_1 += steps[0];

            input_2 += steps[1];

            output += steps[2];

        }

    }

  2. The NumPy part, built by

    char types[3]

    

    types[0] = NPY_BYTE   /* type of first input arg */

    types[1] = NPY_BYTE   /* type of second input arg */

    types[2] = NPY_BYTE   /* type of third input arg */

    

    PyObject *python_ufunc = PyUFunc_FromFuncAndData(

        ufunc_loop,

        NULL,

        types,

        1, /* ntypes */

        2, /* num_inputs */

        1, /* num_outputs */

        identity_element,

        name,

        docstring,

        unused)

    • A ufunc can also support multiple different input-output type combinations.

Making it easier

  1. ufunc_loop is of very generic form, and NumPy provides pre-made ones

    PyUfunc_f_f

    float elementwise_func(float input_1)

    PyUfunc_ff_f

    float elementwise_func(float input_1, float input_2)

    PyUfunc_d_d

    double elementwise_func(double input_1)

    PyUfunc_dd_d

    double elementwise_func(double input_1, double input_2)

    PyUfunc_D_D

    elementwise_func(npy_cdouble *input, npy_cdouble* output)

    PyUfunc_DD_D

    elementwise_func(npy_cdouble *in1, npy_cdouble *in2, npy_cdouble* out)

    • Only elementwise_func needs to be supplied

    • … except when your elementwise function is not in one of the above forms

2.2.2.2. Exercise: building an ufunc from scratch

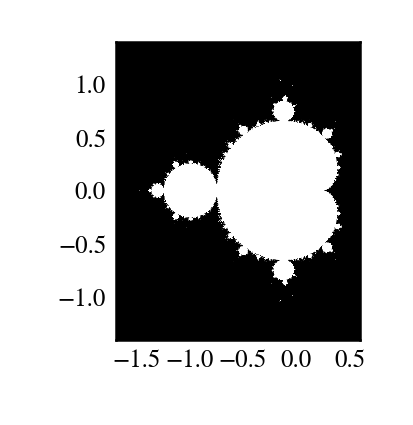
The Mandelbrot fractal is defined by the iteration

z \leftarrow z^2 + c

where c = x + i y is a complex number. This iteration is repeated – if z stays finite no matter how long the iteration runs, c belongs to the Mandelbrot set.

  • Make ufunc called mandel(z0, c) that computes:

    z = z0

    for k in range(iterations):

        z = z*z + c

    say, 100 iterations or until z.real**2 + z.imag**2 > 1000. Use it to determine which c are in the Mandelbrot set.

  • Our function is a simple one, so make use of the PyUFunc_* helpers.

  • Write it in Cython

See also

mandel.pyx, mandelplot.py

Reminder: some pre-made Ufunc loops:

PyUfunc_f_f

float elementwise_func(float input_1)

PyUfunc_ff_f

float elementwise_func(float input_1, float input_2)

PyUfunc_d_d

double elementwise_func(double input_1)

PyUfunc_dd_d

double elementwise_func(double input_1, double input_2)

PyUfunc_D_D

elementwise_func(complex_double *input, complex_double* output)

PyUfunc_DD_D

elementwise_func(complex_double *in1, complex_double *in2, complex_double* out)

Type codes:

NPY_BOOL, NPY_BYTE, NPY_UBYTE, NPY_SHORT, NPY_USHORT, NPY_INT, NPY_UINT,

NPY_LONG, NPY_ULONG, NPY_LONGLONG, NPY_ULONGLONG, NPY_FLOAT, NPY_DOUBLE,

NPY_LONGDOUBLE, NPY_CFLOAT, NPY_CDOUBLE, NPY_CLONGDOUBLE, NPY_DATETIME,

NPY_TIMEDELTA, NPY_OBJECT, NPY_STRING, NPY_UNICODE, NPY_VOID

2.2.2.3. Solution: building an ufunc from scratch

# The elementwise function

# ------------------------



cdef void mandel_single_point(double complex *z_in,

                              double complex *c_in,

                              double complex *z_out) noexcept nogil:

    #

    # The Mandelbrot iteration

    #



    #

    # Some points of note:

    #

    # - It's *NOT* allowed to call any Python functions here.

    #

    #   The Ufunc loop runs with the Python Global Interpreter Lock released.

    #   Hence, the ``nogil``.

    #

    # - And so all local variables must be declared with ``cdef``

    #

    # - Note also that this function receives *pointers* to the data;

    #   the "traditional" solution to passing complex variables around

    #



    cdef double complex z = z_in[0]

    cdef double complex c = c_in[0]

    cdef int k  # the integer we use in the for loop



    # Straightforward iteration



    for k in range(100):

        z = z*z + c

        if z.real**2 + z.imag**2 > 1000:

            break



    # Return the answer for this point

    z_out[0] = z





# Boilerplate Cython definitions

#

# Pulls definitions from the NumPy C headers.

# -------------------------------------------



from numpy cimport import_array, import_ufunc

from numpy cimport (PyUFunc_FromFuncAndData,

                    PyUFuncGenericFunction)

from numpy cimport NPY_CDOUBLE

from numpy cimport PyUFunc_DD_D



# Required module initialization

# ------------------------------



import_array()

import_ufunc()





# The actual ufunc declaration

# ----------------------------



cdef PyUFuncGenericFunction loop_func[1]

cdef char input_output_types[3]

cdef void *elementwise_funcs[1]



loop_func[0] = PyUFunc_DD_D



input_output_types[0] = NPY_CDOUBLE

input_output_types[1] = NPY_CDOUBLE

input_output_types[2] = NPY_CDOUBLE



elementwise_funcs[0] = <void*>mandel_single_point



mandel = PyUFunc_FromFuncAndData(

    loop_func,

    elementwise_funcs,

    input_output_types,

    1, # number of supported input types

    2, # number of input args

    1, # number of output args

    0, # `identity` element, never mind this

    "mandel", # function name

    "mandel(z, c) -> computes iterated z*z + c", # docstring

    0 # unused

    )

"""

Plot Mandelbrot

================



Plot the Mandelbrot ensemble.



"""



import numpy as np

import mandel



x = np.linspace(-1.7, 0.6, 1000)

y = np.linspace(-1.4, 1.4, 1000)

c = x[None, :] + 1j * y[:, None]

z = mandel.mandel(c, c)



import matplotlib.pyplot as plt



plt.imshow(abs(z) ** 2 < 1000, extent=[-1.7, 0.6, -1.4, 1.4])

plt.gray()

plt.show()
../../_images/mandelbrot.png

Note

Most of the boilerplate could be automated by these Cython modules:

https://github.com/cython/cython/wiki/MarkLodato-CreatingUfuncs

Several accepted input types

E.g. supporting both single- and double-precision versions

cdef void mandel_single_point(double complex *z_in,

                              double complex *c_in,

                              double complex *z_out) nogil:

   ...



cdef void mandel_single_point_singleprec(float complex *z_in,

                                         float complex *c_in,

                                         float complex *z_out) nogil:

   ...



cdef PyUFuncGenericFunction loop_funcs[2]

cdef char input_output_types[3*2]

cdef void *elementwise_funcs[1*2]



loop_funcs[0] = PyUFunc_DD_D

input_output_types[0] = NPY_CDOUBLE

input_output_types[1] = NPY_CDOUBLE

input_output_types[2] = NPY_CDOUBLE

elementwise_funcs[0] = <void*>mandel_single_point



loop_funcs[1] = PyUFunc_FF_F

input_output_types[3] = NPY_CFLOAT

input_output_types[4] = NPY_CFLOAT

input_output_types[5] = NPY_CFLOAT

elementwise_funcs[1] = <void*>mandel_single_point_singleprec



mandel = PyUFunc_FromFuncAndData(

    loop_func,

    elementwise_funcs,

    input_output_types,

    2, # number of supported input types   <----------------

    2, # number of input args

    1, # number of output args

    0, # `identity` element, never mind this

    "mandel", # function name

    "mandel(z, c) -> computes iterated z*z + c", # docstring

    0 # unused

    )

2.2.2.4. Generalized ufuncs

ufunc

output = elementwise_function(input)

Both output and input can be a single array element only.

generalized ufunc

output and input can be arrays with a fixed number of dimensions

For example, matrix trace (sum of diag elements):

input shape = (n, n)

output shape = ()      i.e.  scalar



(n, n) -> ()

Matrix product:

input_1 shape = (m, n)

input_2 shape = (n, p)

output shape  = (m, p)



(m, n), (n, p) -> (m, p)

  • This is called the “signature” of the generalized ufunc

  • The dimensions on which the g-ufunc acts, are “core dimensions”

Status in NumPy

  • g-ufuncs are in NumPy already …

  • new ones can be created with PyUFunc_FromFuncAndDataAndSignature

  • most linear-algebra functions are implemented as g-ufuncs to enable working with stacked arrays:

    >>> import numpy as np

    >>> rng = np.random.default_rng(27446968)

    >>> np.linalg.det(rng.random((3, 5, 5)))

    array([ 0.01829761, -0.0077266 , -0.05336566])

    >>> np.linalg._umath_linalg.det.signature

    '(m,m)->()'

  • matrix multiplication this way could be useful for operating on many small matrices at once

  • Also see tensordot and einsum

Generalized ufunc loop

Matrix multiplication (m,n),(n,p) -> (m,p)

void gufunc_loop(void **args, int *dimensions, int *steps, void *data)

{

    char *input_1 = (char*)args[0];  /* these are as previously */

    char *input_2 = (char*)args[1];

    char *output = (char*)args[2];



    int input_1_stride_m = steps[3];  /* strides for the core dimensions */

    int input_1_stride_n = steps[4];  /* are added after the non-core */

    int input_2_strides_n = steps[5]; /* steps */

    int input_2_strides_p = steps[6];

    int output_strides_n = steps[7];

    int output_strides_p = steps[8];



    int m = dimension[1]; /* core dimensions are added after */

    int n = dimension[2]; /* the main dimension; order as in */

    int p = dimension[3]; /* signature */



    int i;



    for (i = 0; i < dimensions[0]; ++i) {

        matmul_for_strided_matrices(input_1, input_2, output,

                                    strides for each array...);



        input_1 += steps[0];

        input_2 += steps[1];

        output += steps[2];

    }

}

2.2.3. Interoperability features

2.2.3.1. Sharing multidimensional, typed data

Suppose you

  1. Write a library than handles (multidimensional) binary data,

  2. Want to make it easy to manipulate the data with NumPy, or whatever other library,

  3. … but would not like to have NumPy as a dependency.

Currently, 3 solutions:

  1. the “old” buffer interface

  2. the array interface

  3. the “new” buffer interface (PEP 3118)

2.2.3.2. The old buffer protocol

  • Only 1-D buffers

  • No data type information

  • C-level interface; PyBufferProcs tp_as_buffer in the type object

  • But it’s integrated into Python (e.g. strings support it)

Mini-exercise using Pillow (Python Imaging Library):

See also

pilbuffer.py

>>> from PIL import Image

>>> data = np.zeros((200, 200, 4), dtype=np.uint8)

>>> data[:, :] = [255, 0, 0, 255] # Red

>>> # In PIL, RGBA images consist of 32-bit integers whose bytes are [RR,GG,BB,AA]

>>> data = data.view(np.int32).squeeze()

>>> img = Image.frombuffer("RGBA", (200, 200), data, "raw", "RGBA", 0, 1)

>>> img.save('test.png')

Q:

Check what happens if data is now modified, and img saved again.

2.2.3.3. The old buffer protocol

"""

From buffer

============



Show how to exchange data between numpy and a library that only knows

the buffer interface.

"""



import numpy as np

from PIL import Image



# Let's make a sample image, RGBA format



x = np.zeros((200, 200, 4), dtype=np.uint8)



x[:, :, 0] = 255  # red

x[:, :, 3] = 255  # opaque



data = x.view(np.int32)  # Check that you understand why this is OK!



img = Image.frombuffer("RGBA", (200, 200), data)

img.save("test.png")



# Modify the original data, and save again.



x[:, :, 1] = 255

img.save("test2.png")
../../_images/test.png ../../_images/test2.png

2.2.3.4. Array interface protocol

  • Multidimensional buffers

  • Data type information present

  • NumPy-specific approach; slowly deprecated (but not going away)

  • Not integrated in Python otherwise

See also

Documentation: https://numpy.org/doc/stable/reference/arrays.interface.html

>>> x = np.array([[1, 2], [3, 4]])

>>> x.__array_interface__   

{'data': (171694552, False),      # memory address of data, is readonly?

 'descr': [('', '<i4')],          # data type descriptor

 'typestr': '<i4',                # same, in another form

 'strides': None,                 # strides; or None if in C-order

 'shape': (2, 2),

 'version': 3,

}
::
>>> from PIL import Image

>>> img = Image.open('data/test.png')

>>> img.__array_interface__

{'version': 3,

 'data': ...,

 'shape': (200, 200, 4),

 'typestr': '|u1'}

>>> x = np.asarray(img)

>>> x.shape

(200, 200, 4)

Note

A more C-friendly variant of the array interface is also defined.

2.2.4. Array siblings: chararray, maskedarray

2.2.4.1. chararray: vectorized string operations

>>> x = np.char.asarray(['a', '  bbb', '  ccc'])

>>> x

chararray(['a', '  bbb', '  ccc'], dtype='<U5')

>>> x.upper()

chararray(['A', '  BBB', '  CCC'], dtype='<U5')

2.2.4.2. masked_array missing data

Masked arrays are arrays that may have missing or invalid entries.

For example, suppose we have an array where the fourth entry is invalid:

>>> x = np.array([1, 2, 3, -99, 5])

One way to describe this is to create a masked array:

>>> mx = np.ma.masked_array(x, mask=[0, 0, 0, 1, 0])

>>> mx

masked_array(data=[1, 2, 3, --, 5],

             mask=[False, False, False,  True, False],

       fill_value=999999)

Masked mean ignores masked data:

>>> mx.mean()

np.float64(2.75)

>>> np.mean(mx)

np.float64(2.75)

Warning

Not all NumPy functions respect masks, for instance np.dot, so check the return types.

The masked_array returns a view to the original array:

>>> mx[1] = 9

>>> x

array([  1,   9,   3, -99,   5])

The mask

You can modify the mask by assigning:

>>> mx[1] = np.ma.masked

>>> mx

masked_array(data=[1, --, 3, --, 5],

             mask=[False,  True, False,  True, False],

       fill_value=999999)

The mask is cleared on assignment:

>>> mx[1] = 9

>>> mx

masked_array(data=[1, 9, 3, --, 5],

             mask=[False, False, False,  True, False],

       fill_value=999999)

The mask is also available directly:

>>> mx.mask

array([False, False, False,  True, False])

The masked entries can be filled with a given value to get an usual array back:

>>> x2 = mx.filled(-1)

>>> x2

array([ 1,  9,  3, -1,  5])

The mask can also be cleared:

>>> mx.mask = np.ma.nomask

>>> mx

masked_array(data=[1, 9, 3, -99, 5],

             mask=[False, False, False, False, False],

       fill_value=999999)

Domain-aware functions

The masked array package also contains domain-aware functions:

>>> np.ma.log(np.array([1, 2, -1, -2, 3, -5]))

masked_array(data=[0.0, 0.693147180559..., --, --, 1.098612288668..., --],

             mask=[False, False,  True,  True, False,  True],

       fill_value=1e+20)

Note

Streamlined and more seamless support for dealing with missing data in arrays is making its way into NumPy 1.7. Stay tuned!

../../_images/sphx_glr_plot_maskedstats_001.png

2.2.4.3. recarray: purely convenience

>>> arr = np.array([('a', 1), ('b', 2)], dtype=[('x', 'S1'), ('y', int)])

>>> arr2 = arr.view(np.recarray)

>>> arr2.x

array([b'a', b'b'], dtype='|S1')

>>> arr2.y

array([1, 2])

2.2.5. Summary

  • Anatomy of the ndarray: data, dtype, strides.

  • Universal functions: elementwise operations, how to make new ones

  • Ndarray subclasses

  • Various buffer interfaces for integration with other tools

  • Recent additions: PEP 3118, generalized ufuncs

2.2.6. Contributing to NumPy/SciPy

2.2.6.1. Why

  • “There’s a bug?”

  • “I don’t understand what this is supposed to do?”

  • “I have this fancy code. Would you like to have it?”

  • “I’d like to help! What can I do?”

2.2.6.2. Reporting bugs

Good bug report

Title: numpy.random.permutations fails for non-integer arguments



I'm trying to generate random permutations, using numpy.random.permutations



When calling numpy.random.permutation with non-integer arguments

it fails with a cryptic error message::



    >>> rng.permutation(12)

    array([ 2,  6,  4,  1,  8, 11, 10,  5,  9,  3,  7,  0])

    >>> rng.permutation(12.) #doctest: +SKIP

    Traceback (most recent call last):

    File "<stdin>", line 1, in <module>

    File "_generator.pyx", line 4844, in numpy.random._generator.Generator.permutation

    numpy.exceptions.AxisError: axis 0 is out of bounds for array of dimension 0



This also happens with long arguments, and so

np.random.permutation(X.shape[0]) where X is an array fails on 64

bit windows (where shape is a tuple of longs).



It would be great if it could cast to integer or at least raise a

proper error for non-integer types.



I'm using NumPy 1.4.1, built from the official tarball, on Windows

64 with Visual studio 2008, on Python.org 64-bit Python.

  1. What are you trying to do?

  2. Small code snippet reproducing the bug (if possible)

    • What actually happens

    • What you’d expect

  3. Platform (Windows / Linux / OSX, 32/64 bits, x86/PPC, …)

  4. Version of NumPy/SciPy

    >>> print(np.__version__)

    2...

    Check that the following is what you expect

    >>> print(np.__file__)

    /...

    In case you have old/broken NumPy installations lying around.

    If unsure, try to remove existing NumPy installations, and reinstall…

2.2.6.3. Contributing to documentation

  1. Documentation editor

    • https://numpy.org/doc/stable/

    • Registration

      • Register an account

      • Subscribe to scipy-dev mailing list (subscribers-only)

      • Problem with mailing lists: you get mail

      • Send a mail @ scipy-dev mailing list; ask for activation:

        To: scipy-dev@scipy.org

        

        Hi,

        

        I'd like to edit NumPy/SciPy docstrings. My account is XXXXX

        

        Cheers,

        N. N.

  2. Edit sources and send patches (as for bugs)

  3. Complain on the mailing list

2.2.6.4. Contributing features

The contribution of features is documented on https://numpy.org/doc/stable/dev/

2.2.6.5. How to help, in general

  • Bug fixes always welcome!

    • What irks you most

    • Browse the tracker

  • Documentation work

  • Ask on communication channels:

    • numpy-discussion list

    • scipy-dev list