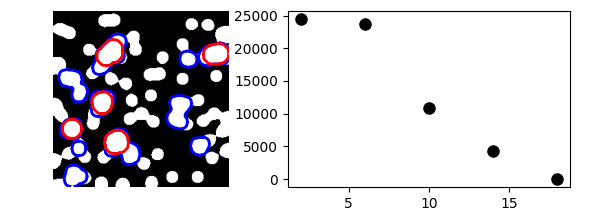
2.6.8.23. Granulometry

This example performs a simple granulometry analysis.

import numpy as np
import scipy as sp
import matplotlib.pyplot as plt


def disk_structure(n):
    struct = np.zeros((2 * n + 1, 2 * n + 1))
    x, y = np.indices((2 * n + 1, 2 * n + 1))
    mask = (x - n) ** 2 + (y - n) ** 2 <= n**2
    struct[mask] = 1
    return struct.astype(bool)


def granulometry(data, sizes=None):
    s = max(data.shape)
    if sizes is None:
        sizes = range(1, s / 2, 2)
    granulo = [
        sp.ndimage.binary_opening(data, structure=disk_structure(n)).sum()
        for n in sizes
    ]
    return granulo


rng = np.random.default_rng(27446968)
n = 10
l = 256
im = np.zeros((l, l))
points = l * rng.random((2, n**2))
im[(points[0]).astype(int), (points[1]).astype(int)] = 1
im = sp.ndimage.gaussian_filter(im, sigma=l / (4.0 * n))

mask = im > im.mean()

granulo = granulometry(mask, sizes=np.arange(2, 19, 4))

plt.figure(figsize=(6, 2.2))

plt.subplot(121)
plt.imshow(mask, cmap="gray")
opened = sp.ndimage.binary_opening(mask, structure=disk_structure(10))
opened_more = sp.ndimage.binary_opening(mask, structure=disk_structure(14))
plt.contour(opened, [0.5], colors="b", linewidths=2)
plt.contour(opened_more, [0.5], colors="r", linewidths=2)
plt.axis("off")
plt.subplot(122)
plt.plot(np.arange(2, 19, 4), granulo, "ok", ms=8)


plt.subplots_adjust(wspace=0.02, hspace=0.15, top=0.95, bottom=0.15, left=0, right=0.95)
plt.show()