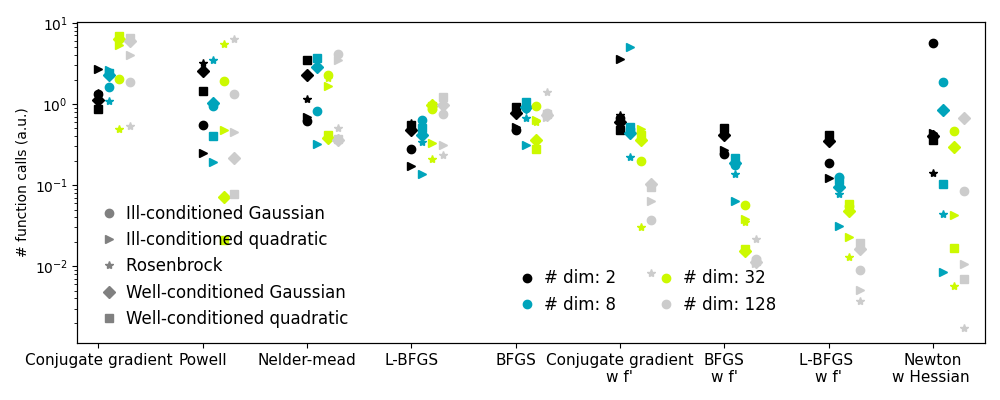
2.7.4.10. Plotting the comparison of optimizers

Plots the results from the comparison of optimizers.

import pickle
import sys

import numpy as np

import matplotlib
import matplotlib.pyplot as plt

results = pickle.load(
    open(f"helper/compare_optimizers_py{sys.version_info[0]}.pkl", "rb")
)
n_methods = len(list(results.values())[0]["Rosenbrock  "])
n_dims = len(results)

symbols = "o>*Ds"

plt.figure(1, figsize=(10, 4))
plt.clf()

nipy_spectral = matplotlib.colormaps["nipy_spectral"]
colors = nipy_spectral(np.linspace(0, 1, n_dims))[:, :3]

method_names = list(list(results.values())[0]["Rosenbrock  "].keys())
method_names.sort(key=lambda x: x[::-1], reverse=True)

for n_dim_index, ((n_dim, n_dim_bench), color) in enumerate(
    zip(sorted(results.items()), colors, strict=True)
):
    for (cost_name, cost_bench), symbol in zip(
        sorted(n_dim_bench.items()), symbols, strict=True
    ):
        for (
            method_index,
            method_name,
        ) in enumerate(method_names):
            this_bench = cost_bench[method_name]
            bench = np.mean(this_bench)
            plt.semilogy(
                [
                    method_index + 0.1 * n_dim_index,
                ],
                [
                    bench,
                ],
                marker=symbol,
                color=color,
            )

# Create a legend for the problem type
for cost_name, symbol in zip(sorted(n_dim_bench.keys()), symbols, strict=True):
    plt.semilogy(
        [
            -10,
        ],
        [
            0,
        ],
        symbol,
        color=".5",
        label=cost_name,
    )

plt.xticks(np.arange(n_methods), method_names, size=11)
plt.xlim(-0.2, n_methods - 0.5)
plt.legend(loc="best", numpoints=1, handletextpad=0, prop={"size": 12}, frameon=False)
plt.ylabel("# function calls (a.u.)")

# Create a second legend for the problem dimensionality
plt.twinx()

for n_dim, color in zip(sorted(results.keys()), colors, strict=True):
    plt.plot(
        [
            -10,
        ],
        [
            0,
        ],
        "o",
        color=color,
        label=f"# dim: {n_dim}",
    )
plt.legend(
    loc=(0.47, 0.07),
    numpoints=1,
    handletextpad=0,
    prop={"size": 12},
    frameon=False,
    ncol=2,
)
plt.xlim(-0.2, n_methods - 0.5)

plt.xticks(np.arange(n_methods), method_names)
plt.yticks(())

plt.tight_layout()
plt.show()