2.5.1. Introduction

(dense) matrix is:

• mathematical object

• data structure for storing a 2D array of values

important features:

• memory allocated once for all items

  • usually a contiguous chunk, think NumPy ndarray

• fast access to individual items (*)

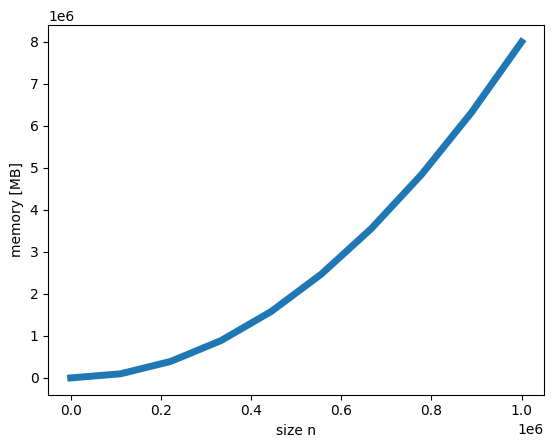
2.5.1.1. Why Sparse Matrices?

• the memory grows like n**2 for dense matrix

• small example (double precision matrix):

  >>> import numpy as np
  >>> import matplotlib.pyplot as plt
  >>> x = np.linspace(0, 1e6, 10)
  >>> plt.plot(x, 8.0 * (x**2) / 1e6, lw=5)
  [<matplotlib.lines.Line2D object at ...>]
  >>> plt.xlabel('size n')
  Text(...'size n')
  >>> plt.ylabel('memory [MB]')
  Text(...'memory [MB]')
  

2.5.1.2. Sparse Matrices vs. Sparse Matrix Storage Schemes

• sparse matrix is a matrix, which is almost empty

• storing all the zeros is wasteful -> store only nonzero items

• think compression

• pros: huge memory savings

• cons: slow access to individual items, but it depends on actual storage scheme.

2.5.1.3. Typical Applications

• solution of partial differential equations (PDEs)

  • the finite element method

  • mechanical engineering, electrotechnics, physics, …

• graph theory

  • nonzero at (i, j) means that node i is connected to node j

• natural language processing

  • nonzero at (i, j) means that the document i contains the word j

• …

2.5.1.4. Prerequisites

• numpy

• scipy

• matplotlib (optional)

• ipython (the enhancements come handy)

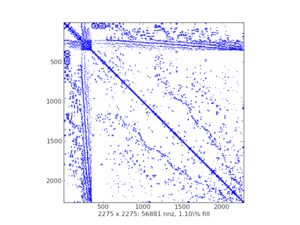
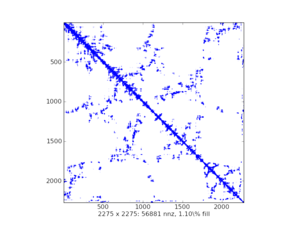
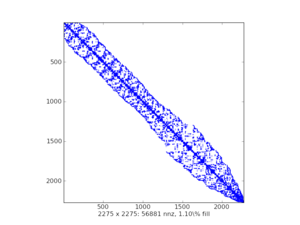
2.5.1.5. Sparsity Structure Visualization

• spy() from matplotlib

• example plots: