2.7.4.7. Brent’s method

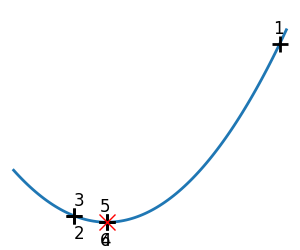
Illustration of 1D optimization: Brent’s method

• 
• 
• 
• 

Converged at  6
Converged at  23

import numpy as np
import matplotlib.pyplot as plt
import scipy as sp

x = np.linspace(-1, 3, 100)
x_0 = np.exp(-1)


def f(x):
    return (x - x_0) ** 2 + epsilon * np.exp(-5 * (x - 0.5 - x_0) ** 2)


for epsilon in (0, 1):
    plt.figure(figsize=(3, 2.5))
    plt.axes((0, 0, 1, 1))

    # A convex function
    plt.plot(x, f(x), linewidth=2)

    # Apply brent method. To have access to the iteration, do this in an
    # artificial way: allow the algorithm to iter only once
    all_x = []
    all_y = []
    for iter in range(30):
        result = sp.optimize.minimize_scalar(
            f,
            bracket=(-5, 2.9, 4.5),
            method="Brent",
            options={"maxiter": iter},
            tol=np.finfo(1.0).eps,
        )
        if result.success:
            print("Converged at ", iter)
            break

        this_x = result.x
        all_x.append(this_x)
        all_y.append(f(this_x))
        if iter < 6:
            plt.text(
                this_x - 0.05 * np.sign(this_x) - 0.05,
                f(this_x) + 1.2 * (0.3 - iter % 2),
                str(iter + 1),
                size=12,
            )

    plt.plot(all_x[:10], all_y[:10], "k+", markersize=12, markeredgewidth=2)

    plt.plot(all_x[-1], all_y[-1], "rx", markersize=12)
    plt.axis("off")
    plt.ylim(ymin=-1, ymax=8)

    plt.figure(figsize=(4, 3))
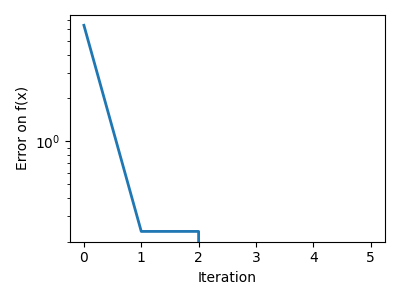
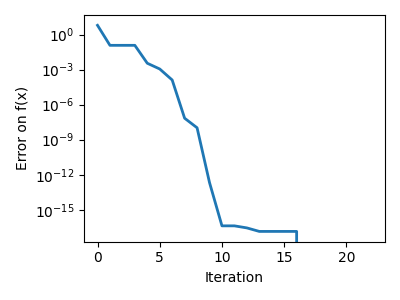
    plt.semilogy(np.abs(all_y - all_y[-1]), linewidth=2)
    plt.ylabel("Error on f(x)")
    plt.xlabel("Iteration")
    plt.tight_layout()

plt.show()