3.1.6.6. Test for an education/gender interaction in wages

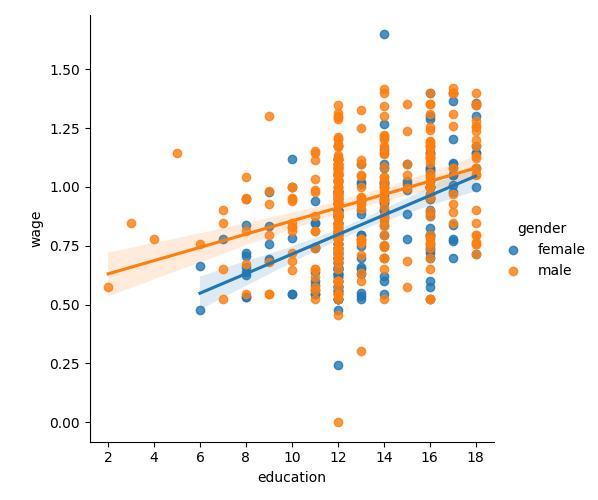
Wages depend mostly on education. Here we investigate how this dependence is related to gender: not only does gender create an offset in wages, it also seems that wages increase more with education for males than females.

Does our data support this last hypothesis? We will test this using statsmodels’ formulas (http://statsmodels.sourceforge.net/stable/example_formulas.html).

Load and massage the data

import pandas

import urllib.request
import os

if not os.path.exists("wages.txt"):
    # Download the file if it is not present
    url = "http://lib.stat.cmu.edu/datasets/CPS_85_Wages"
    with urllib.request.urlopen(url) as r, open("wages.txt", "wb") as f:
        f.write(r.read())

# EDUCATION: Number of years of education
# SEX: 1=Female, 0=Male
# WAGE: Wage (dollars per hour)
data = pandas.read_csv(
    "wages.txt",
    skiprows=27,
    skipfooter=6,
    sep=None,
    header=None,
    names=["education", "gender", "wage"],
    usecols=[0, 2, 5],
)

# Convert genders to strings (this is particularly useful so that the
# statsmodels formulas detects that gender is a categorical variable)
import numpy as np

data["gender"] = np.choose(data.gender, ["male", "female"])

# Log-transform the wages, because they typically are increased with
# multiplicative factors
data["wage"] = np.log10(data["wage"])

/home/runner/work/scientific-python-lectures/scientific-python-lectures/packages/statistics/examples/plot_wage_education_gender.py:32: ParserWarning: Falling back to the 'python' engine because the 'c' engine does not support skipfooter; you can avoid this warning by specifying engine='python'.
  data = pandas.read_csv(

simple plotting

import seaborn

# Plot 2 linear fits for male and female.
seaborn.lmplot(y="wage", x="education", hue="gender", data=data)

<seaborn.axisgrid.FacetGrid object at 0x7fe9cb119790>

statistical analysis

import statsmodels.formula.api as sm

# Note that this model is not the plot displayed above: it is one
# joined model for male and female, not separate models for male and
# female. The reason is that a single model enables statistical testing
result = sm.ols(formula="wage ~ education + gender", data=data).fit()
print(result.summary())

                            OLS Regression Results
==============================================================================
Dep. Variable:                   wage   R-squared:                       0.193
Model:                            OLS   Adj. R-squared:                  0.190
Method:                 Least Squares   F-statistic:                     63.42
Date:                Tue, 17 Dec 2024   Prob (F-statistic):           2.01e-25
Time:                        02:24:01   Log-Likelihood:                 86.654
No. Observations:                 534   AIC:                            -167.3
Df Residuals:                     531   BIC:                            -154.5
Df Model:                           2
Covariance Type:            nonrobust
==================================================================================
                     coef    std err          t      P>|t|      [0.025      0.975]
----------------------------------------------------------------------------------
Intercept          0.4053      0.046      8.732      0.000       0.314       0.496
gender[T.male]     0.1008      0.018      5.625      0.000       0.066       0.136
education          0.0334      0.003      9.768      0.000       0.027       0.040
==============================================================================
Omnibus:                        4.675   Durbin-Watson:                   1.792
Prob(Omnibus):                  0.097   Jarque-Bera (JB):                4.876
Skew:                          -0.147   Prob(JB):                       0.0873
Kurtosis:                       3.365   Cond. No.                         69.7
==============================================================================

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

The plots above highlight that there is not only a different offset in wage but also a different slope

We need to model this using an interaction

result = sm.ols(
    formula="wage ~ education + gender + education * gender", data=data
).fit()
print(result.summary())

                            OLS Regression Results
==============================================================================
Dep. Variable:                   wage   R-squared:                       0.198
Model:                            OLS   Adj. R-squared:                  0.194
Method:                 Least Squares   F-statistic:                     43.72
Date:                Tue, 17 Dec 2024   Prob (F-statistic):           2.94e-25
Time:                        02:24:01   Log-Likelihood:                 88.503
No. Observations:                 534   AIC:                            -169.0
Df Residuals:                     530   BIC:                            -151.9
Df Model:                           3
Covariance Type:            nonrobust
============================================================================================
                               coef    std err          t      P>|t|      [0.025      0.975]
--------------------------------------------------------------------------------------------
Intercept                    0.2998      0.072      4.173      0.000       0.159       0.441
gender[T.male]               0.2750      0.093      2.972      0.003       0.093       0.457
education                    0.0415      0.005      7.647      0.000       0.031       0.052
education:gender[T.male]    -0.0134      0.007     -1.919      0.056      -0.027       0.000
==============================================================================
Omnibus:                        4.838   Durbin-Watson:                   1.825
Prob(Omnibus):                  0.089   Jarque-Bera (JB):                5.000
Skew:                          -0.156   Prob(JB):                       0.0821
Kurtosis:                       3.356   Cond. No.                         194.
==============================================================================

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

Looking at the p-value of the interaction of gender and education, the data does not support the hypothesis that education benefits males more than female (p-value > 0.05).

import matplotlib.pyplot as plt

plt.show()