sympy : Symbolic Mathematics in Python#
Author: Fabian Pedregosa
Objectives
Evaluate expressions with arbitrary precision.
Perform algebraic manipulations on symbolic expressions.
Perform basic calculus tasks (limits, differentiation and : integration) with symbolic expressions.
Solve polynomial and transcendental equations.
Solve some differential equations.
What is SymPy? SymPy is a Python library for symbolic mathematics. It aims to be an alternative to systems such as Mathematica or Maple while keeping the code as simple as possible and easily extensible. SymPy is written entirely in Python and does not require any external libraries.
Sympy documentation and packages for installation can be found on https://www.sympy.org/
First Steps with SymPy#
Using SymPy as a calculator#
SymPy defines three numerical types: Real, Rational and Integer.
The Rational class represents a rational number as a pair of two
Integers: the numerator and the denominator, so Rational(1, 2)
represents 1/2, Rational(5, 2) 5/2 and so on:
import sympy as sym
a = sym.Rational(1, 2)
a
a*2
SymPy uses mpmath in the background, which makes it possible to perform computations using arbitrary-precision arithmetic. That way, some special constants, like \(e\), \(pi\), \(oo\) (Infinity), are treated as symbols and can be evaluated with arbitrary precision:
sym.pi**2
sym.pi.evalf()
(sym.pi + sym.exp(1)).evalf()
as you see, evalf evaluates the expression to a floating-point number.
There is also a class representing mathematical infinity, called
oo:
sym.oo > 99999
sym.oo + 1
Exercise 63
Calculate \(\sqrt{2}\) with 100 decimals.
Calculate \(1/2 + 1/3\) in rational arithmetic.
Symbols#
In contrast to other Computer Algebra Systems, in SymPy you have to declare symbolic variables explicitly:
x = sym.Symbol('x')
y = sym.Symbol('y')
Then you can manipulate them:
x + y + x - y
(x + y) ** 2
Symbols can now be manipulated using some of python operators: +, -,
*, ** (arithmetic), &, |, ~, >>, << (boolean).
Printing
Sympy allows for control of the display of the output. From here we use the following setting for printing:
sym.init_printing(use_unicode=False, wrap_line=True)
Algebraic manipulations
SymPy is capable of performing powerful algebraic manipulations. We’ll take a look into some of the most frequently used: expand and simplify.
Expand
Use this to expand an algebraic expression. It will try to denest powers and multiplications:
sym.expand((x + y) ** 3)

3 * x * y ** 2 + 3 * y * x ** 2 + x ** 3 + y ** 3

Further options can be given in form on keywords:
sym.expand(x + y, complex=True)
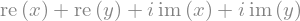
sym.I * sym.im(x) + sym.I * sym.im(y) + sym.re(x) + sym.re(y)
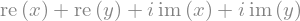
sym.expand(sym.cos(x + y), trig=True)

sym.cos(x) * sym.cos(y) - sym.sin(x) * sym.sin(y)

Simplify#
Use simplify if you would like to transform an expression into a simpler form:
sym.simplify((x + x * y) / x)

Simplification is a somewhat vague term, and more precises
alternatives to simplify exists: powsimp (simplification of
exponents), trigsimp (for trigonometric expressions) , logcombine,
radsimp, together.
Exercise 64
Calculate the expanded form of \((x+y)^6\).
Simplify the trigonometric expression \(\sin(x) / \cos(x)\)
Calculus#
Limits#
Limits are easy to use in SymPy, they follow the syntax limit(function, variable, point), so to compute the limit of \(f(x)\) as
\(x \rightarrow 0\), you would issue limit(f, x, 0):
sym.limit(sym.sin(x) / x, x, 0)

you can also calculate the limit at infinity:
sym.limit(x, x, sym.oo)

sym.limit(1 / x, x, sym.oo)

sym.limit(x ** x, x, 0)

Differentiation#
You can differentiate any SymPy expression using diff(func, var). Examples:
sym.diff(sym.sin(x), x)
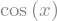
sym.diff(sym.sin(2 * x), x)
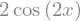
sym.diff(sym.tan(x), x)
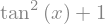
You can check that it is correct by:
sym.limit((sym.tan(x + y) - sym.tan(x)) / y, y, 0)
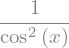
Which is equivalent since
You can check this as well:
sym.trigsimp(sym.diff(sym.tan(x), x))
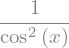
Higher derivatives can be calculated using the diff(func, var, n) method:
sym.diff(sym.sin(2 * x), x, 1)
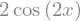
sym.diff(sym.sin(2 * x), x, 2)

sym.diff(sym.sin(2 * x), x, 3)

Series expansion#
SymPy also knows how to compute the Taylor series of an expression at
a point. Use series(expr, var):
sym.series(sym.cos(x), x)
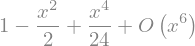
sym.series(1/sym.cos(x), x)
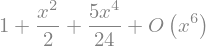
Exercise 65
Calculate \(\lim_{x\rightarrow 0} \sin(x)/x\)
Calculate the derivative of \(log(x)\) for \(x\).
Integration#
SymPy has support for indefinite and definite integration of transcendental
elementary and special functions via integrate() facility, which uses
the powerful extended Risch-Norman algorithm and some heuristics and pattern
matching. You can integrate elementary functions:
sym.integrate(6 * x ** 5, x)
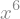
sym.integrate(sym.sin(x), x)

sym.integrate(sym.log(x), x)
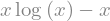
sym.integrate(2 * x + sym.sinh(x), x)

Also special functions are handled easily:
sym.integrate(sym.exp(-x ** 2) * sym.erf(x), x)
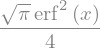
It is possible to compute definite integral:
sym.integrate(x**3, (x, -1, 1))

sym.integrate(sym.sin(x), (x, 0, sym.pi / 2))

sym.integrate(sym.cos(x), (x, -sym.pi / 2, sym.pi / 2))
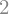
Also improper integrals are supported as well:
sym.integrate(sym.exp(-x), (x, 0, sym.oo))

sym.integrate(sym.exp(-x ** 2), (x, -sym.oo, sym.oo))

Equation solving#
SymPy is able to solve algebraic equations, in one and several
variables using solveset():
sym.solveset(x ** 4 - 1, x)
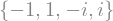
As you can see it takes as first argument an expression that is supposed to be equaled to 0. It also has (limited) support for transcendental equations:
sym.solveset(sym.exp(x) + 1, x)

Systems of linear equations
Sympy is able to solve a large part of
polynomial equations, and is also capable of solving multiple
equations with respect to multiple variables giving a tuple as second
argument. To do this you use the solve() command:
solution = sym.solve((x + 5 * y - 2, -3 * x + 6 * y - 15), (x, y))
solution[x], solution[y]
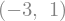
Another alternative in the case of polynomial equations is
factor. factor returns the polynomial factorized into irreducible
terms, and is capable of computing the factorization over various
domains:
f = x ** 4 - 3 * x ** 2 + 1
sym.factor(f)
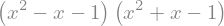
sym.factor(f, modulus=5)
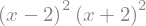
SymPy is also able to solve boolean equations, that is, to decide if a certain boolean expression is satisfiable or not. For this, we use the function satisfiable:
sym.satisfiable(x & y)
{x: True, y: True}
This tells us that (x & y) is True whenever x and y are both True.
If an expression cannot be true, i.e. no values of its arguments can make
the expression True, it will return False:
sym.satisfiable(x & ~x)
False
Exercise 66
Solve the system of equations \(x + y = 2\), \(2\cdot x + y = 0\)
Are there boolean values
x,ythat make(~x | y) & (~y | x)true?
Linear Algebra#
Matrices#
Matrices are created as instances from the Matrix class:
sym.Matrix([[1, 0], [0, 1]])

unlike a NumPy array, you can also put Symbols in it:
x, y = sym.symbols('x, y')
A = sym.Matrix([[1, x], [y, 1]])
A
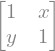
A**2
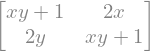
Differential Equations#
SymPy is capable of solving (some) Ordinary Differential. To solve differential equations, use dsolve. First, create an undefined function by passing cls=Function to the symbols function:
f, g = sym.symbols('f g', cls=sym.Function)
f and g are now undefined functions. We can call f(x), and it will represent an unknown function:
f(x)
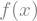
f(x).diff(x, x) + f(x)
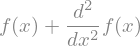
sym.dsolve(f(x).diff(x, x) + f(x), f(x))
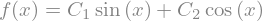
Keyword arguments can be given to this function in order to help if
find the best possible resolution system. For example, if you know
that it is a separable equations, you can use keyword hint='separable'
to force dsolve to resolve it as a separable equation:
sym.dsolve(sym.sin(x) * sym.cos(f(x)) + sym.cos(x) * sym.sin(f(x)) * f(x).diff(x), f(x), hint='separable')
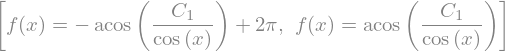
Exercise 67
Solve the Bernoulli differential equation
\[ x \frac{d f(x)}{x} + f(x) - f(x)^2=0 \]Solve the same equation using
hint='Bernoulli'. What do you observe ?

