Advanced operations#
Polynomials#
NumPy also contains polynomials in different bases:
For example, \(3x^2 + 2x - 1\):
import numpy as np
import matplotlib.pyplot as plt
p = np.poly1d([3, 2, -1])
p(0)
np.int64(-1)
p.roots
array([-1. , 0.33333333])
p.order
2
x = np.linspace(0, 1, 20)
rng = np.random.default_rng()
y = np.cos(x) + 0.3*rng.random(20)
p = np.poly1d(np.polyfit(x, y, 3))
t = np.linspace(0, 1, 200) # use a larger number of points for smoother plotting
plt.plot(x, y, 'o', t, p(t), '-');
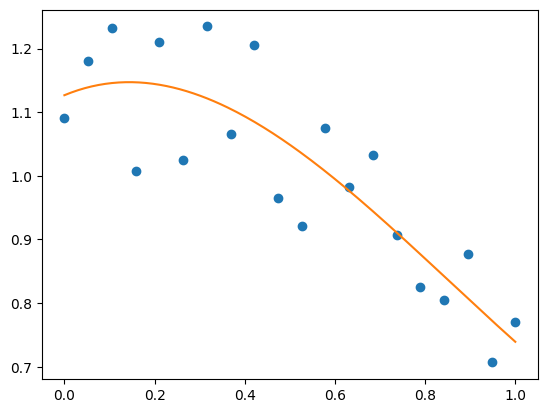
See https://numpy.org/doc/stable/reference/routines.polynomials.poly1d.html for more.
More polynomials (with more bases)#
NumPy also has a more sophisticated polynomial interface, which supports e.g. the Chebyshev basis.
\(3x^2 + 2x - 1\):
p = np.polynomial.Polynomial([-1, 2, 3]) # coefs in different order!
p(0)
np.float64(-1.0)
p.roots()
array([-1. , 0.33333333])
p.degree() # In general polynomials do not always expose 'order'
2
Example using polynomials in Chebyshev basis, for polynomials in
range [-1, 1]:
x = np.linspace(-1, 1, 2000)
rng = np.random.default_rng()
y = np.cos(x) + 0.3*rng.random(2000)
p = np.polynomial.Chebyshev.fit(x, y, 90)
plt.plot(x, y, 'r.')
plt.plot(x, p(x), 'k-', lw=3)
[<matplotlib.lines.Line2D at 0x7f000ce8f3b0>]
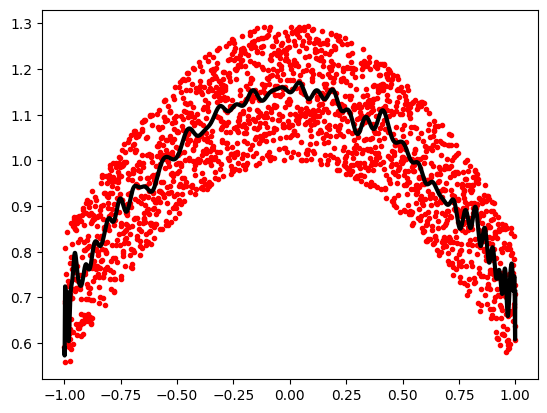
The Chebyshev polynomials have some advantages in interpolation.
Loading data files#
Text files#
Example: populations.txt.
data = np.loadtxt('data/populations.txt')
data
array([[ 1900., 30000., 4000., 48300.],
[ 1901., 47200., 6100., 48200.],
[ 1902., 70200., 9800., 41500.],
[ 1903., 77400., 35200., 38200.],
[ 1904., 36300., 59400., 40600.],
[ 1905., 20600., 41700., 39800.],
[ 1906., 18100., 19000., 38600.],
[ 1907., 21400., 13000., 42300.],
[ 1908., 22000., 8300., 44500.],
[ 1909., 25400., 9100., 42100.],
[ 1910., 27100., 7400., 46000.],
[ 1911., 40300., 8000., 46800.],
[ 1912., 57000., 12300., 43800.],
[ 1913., 76600., 19500., 40900.],
[ 1914., 52300., 45700., 39400.],
[ 1915., 19500., 51100., 39000.],
[ 1916., 11200., 29700., 36700.],
[ 1917., 7600., 15800., 41800.],
[ 1918., 14600., 9700., 43300.],
[ 1919., 16200., 10100., 41300.],
[ 1920., 24700., 8600., 47300.]])
np.savetxt('pop2.txt', data)
data2 = np.loadtxt('pop2.txt')
Note
If you have a complicated text file, what you can try are:
np.genfromtxtUsing Python’s I/O functions and e.g. regexps for parsing (Python is quite well suited for this)
Images#
Using Matplotlib:
img = plt.imread('data/elephant.png')
img.shape, img.dtype
((200, 300, 3), dtype('float32'))
# Plot and save the original figure
plt.imshow(img)
plt.savefig('plot.png')
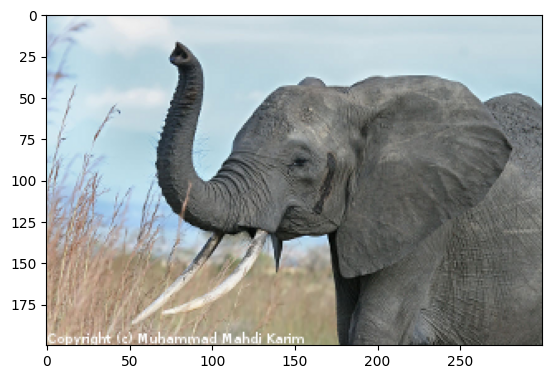
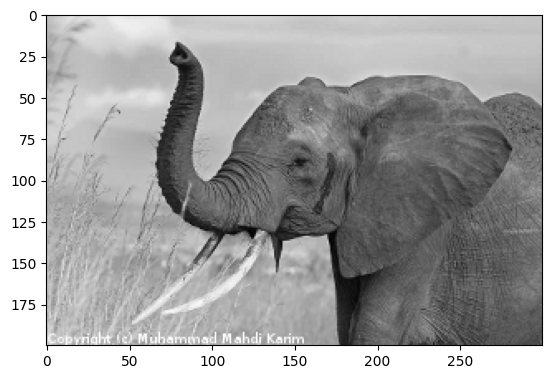
# Plot and save the red channel of the image.
plt.imsave('red_elephant.png', img[:,:,0], cmap=plt.cm.gray)
This saved only one channel (of RGB):
plt.imshow(plt.imread('red_elephant.png'))
<matplotlib.image.AxesImage at 0x7f0012714cb0>
Other libraries:
import imageio.v3 as iio
# Lower resolution (every sixth pixel in each dimension).
iio.imwrite('tiny_elephant.png', (img[::6,::6] * 255).astype(np.uint8))
plt.imshow(plt.imread('tiny_elephant.png'), interpolation='nearest')
<matplotlib.image.AxesImage at 0x7f000ceb9910>
NumPy’s own format#
NumPy has its own binary format, not portable but with efficient I/O:
data = np.ones((3, 3))
np.save('pop.npy', data)
data3 = np.load('pop.npy')
Well-known (& more obscure) file formats#
NetCDF:
scipy.io.netcdf_file, netcdf4-python, …Matlab:
scipy.io.loadmat,scipy.io.savematMatrixMarket:
scipy.io.mmread,scipy.io.mmwriteIDL:
scipy.io.readsav
… if somebody uses it, there’s probably also a Python library for it.
Exercise 21
Write code that loads data from populations.txt: and drops the last column and the first 5 rows. Save
the smaller dataset to pop2.txt.
Solution to Exercise 21
data = np.loadtxt("data/populations.txt")
reduced_data = data[5:, :-1]
np.savetxt("pop2.txt", reduced_data)
NumPy internals
If you are interested in the NumPy internals, there is a good discussion in Advanced NumPy.

